terça-feira, 24 de abril de 2018
Ângulo formado pelos ponteiros do relógio
Macete!
Quando é solicitado o ângulo formado entre os ponteiros da hora e dos minutos, podemos resolver a questão usando a seguinte formula:

(UFRRJ) Considere um relógio cujos ponteiros movi-mentam-se proporcionalmente.
Calcule o valor em graus do menor ângulo formado pelos ponteiros quando esse relógio marcar 14:45h.
Calcule o valor em graus do menor ângulo formado pelos ponteiros quando esse relógio marcar 14:45h.
Solução: Pela fórmula temos:

Dica! Quando o valor da hora é acima de 12h, podemos considerar seu valor congruente; no exemplo anterior se considerarmos 2h 45min, teremos:

Como o ângulo pedido é o menor, temos que calcular o replemento: 360 – 187,5 = 172,5º ou 172º 30´
Ângulos – Geometria Básica
(UFMG) Na figura, OM é a bissetriz do ângulo AOB, ON é a bissetriz do ângulo BOC e OP é a bissetriz do ângulo COD. A soma POD + MON é igual a:


Retas paralelas cortadas por uma transversal
Macete! Regra do Z: Os ângulos formados pela letra “Z” (direita ou invertida) são sempre congruentes.
Macete! Regra do Z: Os ângulos formados pela letra “Z” (direita ou invertida) são sempre congruentes.

(FUVEST) Na figura, as retas r e s são paralelas, o ângulo 1 mede 45º e ângulo 3 mede 55º.
A medida, em graus, do ângulo 2 é:
A medida, em graus, do ângulo 2 é:

a) 50º
b) 55º
c) 60º
d) 80º
e) 100º
b) 55º
c) 60º
d) 80º
e) 100º
Solução: Traçando uma reta auxiliar paralela às outras duas, teremos que o ângulo do meio é igual a soma dos ângulos extremos; com isso temos que:

x = 45º + 55º
x = 100º
Letra e)
x = 100º
Letra e)
Ângulos – Geometria Básica
Tipos de Ângulos
a) Ângulo Agudo: 0º < A < 90º
a) Ângulo Agudo: 0º < A < 90º
b) Ângulo Reto: A = 90º
c) Ângulo Obtuso: 90º < A < 180º
d) Ângulo Raso ou Meia Volta: A = 180º
e) Ângulos Opostos pelo Vértice (OPV): São congru-entes os ângulos AOC e BOD.
f) Ângulos Consecutivos: Possuem um lado e um vértice em comum.
Exemplos: ângulos AOB e AOC; AOB e BOC.
Exemplos: ângulos AOB e AOC; AOB e BOC.
g) Ângulos Adjacentes: São ângulos consecutivos que não possuem pontos internos em comum.
Exemplo: ângulos AOB e BOC.
Exemplo: ângulos AOB e BOC.
h) Ângulos Complementares: Ângulos que somados resultam em 90º.
OBS: Complemento de um ângulo é o valor que falta para a soma completar 90º.
OBS: Complemento de um ângulo é o valor que falta para a soma completar 90º.
i) Ângulos Suplementares: Ângulos que somados seu valor resulta em 180º.
OBS: Suplemento de um ângulo é o valor que falta para a soma completar 180º.
OBS: Suplemento de um ângulo é o valor que falta para a soma completar 180º.
j) Ângulos Replementares: Ângulos que somados resultam em 360º.
OBS: Replemento de um ângulo é o valor que falta para a soma completar 360º.
OBS: Replemento de um ângulo é o valor que falta para a soma completar 360º.

Ângulos – Geometria Básica
São regiões formadas por duas semi-retas com um ponto O em comum chamado origem. Os dois princi-pais sistemas de medidas são:
Circular Sua unidade principal é o radiano (rad); tem como base o ângulo central de uma circunferência cujo arco tem a mesma medida do raio.
Sexagesimal Sua unidade principal é o grau ( º ); tem como base a divisão da circunferência em 360 partes iguais, sendo cada uma dessas partes um grau.
Possui os submúltiplos minuto( ’ ) e segundo ( ” ), cujas equivalências são: 1º = 60’e 1’ = 60″.
Possui os submúltiplos minuto( ’ ) e segundo ( ” ), cujas equivalências são: 1º = 60’e 1’ = 60″.
Relação entre os sistemas

terça-feira, 17 de abril de 2018

 As tampas dos esgotos são circulares e não quadradas, porque uma tampa de esgoto quadrada poderia escorregar pelo buraco e cair dentro do esgoto, quando a voltássemos de lado.
As tampas dos esgotos são circulares e não quadradas, porque uma tampa de esgoto quadrada poderia escorregar pelo buraco e cair dentro do esgoto, quando a voltássemos de lado. O maior sólido geométrico feito pelo homem é a pirâmide de Quéops, no Egito e foi construída no século 25 a.C..
O maior sólido geométrico feito pelo homem é a pirâmide de Quéops, no Egito e foi construída no século 25 a.C..
Esta construção é uma das "sete maravilhas do mundo" que chegou quase intacta aos nossos dias.
Tem de altura 138m e a base quadrada tem de lado 230m. Cobre uma área de 54000 m2 e foi feita com mais de dois milhões de blocos de pedra, pesando cada um deles, em média, 2,5 toneladas.
Segundo o historiador grego Heródoto, esta pirâmide, cujas faces laterais são triângulos isósceles, possui a seguinte propriedade: "Cada face lateral triangular tem uma área igual à do quadrado construído sobre a altura da pirâmide."
Os egípcios construíram cerca de 80 estruturas do tipo desta pirâmide.
A célebre frase que Napoleão disse aos seus soldados aquando da conquista do Egito foi: "Soldados, do alto destas pirâmides quarenta séculos vos contemplam."

 Outra pirâmide célebre construída nos nossos dias, ou melhor, em 1988, é a pirâmide de Louvre que tem de altura 21m e a base quadrada tem 34m de lado.
Outra pirâmide célebre construída nos nossos dias, ou melhor, em 1988, é a pirâmide de Louvre que tem de altura 21m e a base quadrada tem 34m de lado. De entre todas as figuras planas com o mesmo perímetro, o círculo é a que tem maior área.
De entre todas as figuras planas com o mesmo perímetro, o círculo é a que tem maior área. O lançamento de um projétil sobre o qual atue somente a força da gravidade tem uma trajetória parabólica.
O lançamento de um projétil sobre o qual atue somente a força da gravidade tem uma trajetória parabólica. A trajetória de uma partícula alfa no campo electromagnético do núcleo de um átomo traduz-se por uma hipérbole.
A trajetória de uma partícula alfa no campo electromagnético do núcleo de um átomo traduz-se por uma hipérbole. Nos tempos primitivos da civilização grega, foi usado pelos gregos o triângulo de descarga, uma construção que permitia descarregar as pressões exercidas por grandes pesos que se encontravam por cima das portas dos túmulos e das cidadelas.
Nos tempos primitivos da civilização grega, foi usado pelos gregos o triângulo de descarga, uma construção que permitia descarregar as pressões exercidas por grandes pesos que se encontravam por cima das portas dos túmulos e das cidadelas.
Devido ao peso, as portas podiam abater, mas, com o triângulo esse peso era suportado pelos postes laterais que eram maciços. Os triângulos de descarga eram geralmente abertos, mas podiam ser tapados e decorados, como acontece no caso da cidade de Micenas com a porta dos leões.
 Na Expo 98, no pavilhão da Suíça, podíamos ver um hipercubo.
Na Expo 98, no pavilhão da Suíça, podíamos ver um hipercubo.Geometria espacial
Pontos, retas e planos
Na geometria espacial, são conceitos primitivos (e, portanto, aceitos sem definição) os conceitos de ponto, reta e plano. Habitualmente, usamos a seguinte notação:
- Pontos: letras maiúsculas do nosso alfabeto
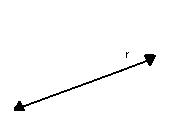
- Retas: letras minúsculas do nosso alfabeto
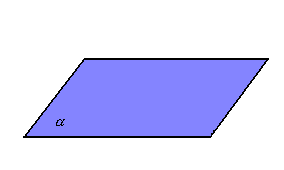
- Planos: letras minúsculas do alfabeto grego
Observação: Espaço é o conjunto de todos os pontos.
Por exemplo, da figura a seguir, podemos escrever:
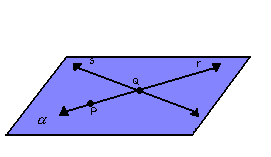 | 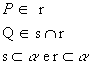 |
Assinar:
Postagens (Atom)